InterIUT 2025 | Write-Ups de mes challenges
Cet article contient les write-ups de mes challenges pour l’InterIUT 2025, c.-à-d. :
- [Reverse] “bzhash”, difficulté : Facile ;
- [Crypto] “Revenu de Solidarité Active (RSA)”, difficulté : Très facile ;
- [Crypto] “lowtropy”, difficulté : Facile ;
- [Crypto] “C’est toi l’OTP !”, difficulté : Difficile.
[Reverse] “bzhash”, difficulté : Facile
Après rétro-ingénierie du binaire “bzhash”, nous comprenons qu’il faut trouver une 2de préimage de la valeur “J’adore la crypto” pour la fonction de hachage implémentée dans le binaire.
Plus précisément, nous comprenons que la fonction opère de la façon suivante :
- Une chaîne d’octets $I$ est donnée en input.
- Une fonction de “padding” (à peu près PKCS#7) la transforme en $I’$ tel que
len(I') % 4 == 0. - La chaine $I’$ est découpée en bloc de $4$ caractères.
- La somme XOR de ces blocs est effectuée afin de créer $H$, en Python on pourrait écrire :
H = xor(*[I_prime[i:i+4] for i in range(0, len(I_prime), 4)]).
Une fois le fonctionnement de la fonction de hachage compris, il est assez facile de trouver une seconde préimage car cette fonction est vraiment pourrie, voici trois méthodes (il en existe sûrement d’autres !) :
- Ajouter un bloc de 4 nullbytes à la fin de
pad("J'adore la crypto"). - Ajouter deux blocs identiques à la fin de
pad("J'adore la crypto")afin que leur somme XOR se compense. - La solution honteuse : ajouter des données random jusqu’à ce que ce soit bon ; la taille du bloc étant très petite ça se brute force
L’implémentation de la solution (1.) et (2.) :
1
2
echo "4a2761646f7265206c612063727970746f03030300000000" | xxd -r -p | ./bzhash
echo "4a2761646f7265206c612063727970746f0303030101010101010101" | xxd -r -p | ./bzhash
[Crypto] “Revenu de Solidarité Active (RSA)”, difficulté : Très facile
TL;DR le fichier chal.py chiffre le flag ($m$) en faisant : $c = m^{-1} \pmod{n}$. Il suffit de ré-inverser $c$ et de retirer le padding afin de retrouver le flag.
En effet, lorsque nous donnons un exposant négatif à la fonction pow() de Python ($-1$ dans notre cas), cette dernière n’effectue pas d’exponentiation modulaire pour la valeur $-1 \pmod{n}$ mais effectue un inverse modulaire ; ce qui est trivial a inverser.
Voici l’implémentation de la solution en Python :
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
from sys import argv
if len(argv) != 2:
print("Usage : python solve.py out-path.txt")
exit()
out = open(argv[1])
nc = []
while ( (l := out.readline()) != ""):
nc.append(int(l.split("= ")[1]))
n, c = nc
e = -1
m = pow(c, e, n)
m = m.to_bytes((m.bit_length() + 7) // 8)
m = m[:m.find(b"}")+1].decode()
print(m)
[Crypto] “lowtropy”, difficulté : Facile
TL;DR Malgré l’utilisation de PBKDF2, l’entropie d’un code PIN est bien plus faible que celle d’un mot de passe, il ne faut donc pas les stocker de la même manière.
Une attaque par recherche exhaustive est donc possible, voici la commande hashcat (cf. doc hashcat) a utiliser pour cracker ce hash :
1
2
echo "sha256:10000:fe+WzU0xXSviLbSZVTGd3WR42SdADxTeXy0i8JR5k7g=:QEViJ8jx0kF3ARzk1Ya4UmQD4HpclbmXsGJ6ZABMnzI=" > /tmp/hash.txt
hashcat -m 10900 -a 3 /tmp/hash.txt ?d?d?d?d?d?d
[Crypto] “C’est toi l’OTP !”, difficulté : Difficile
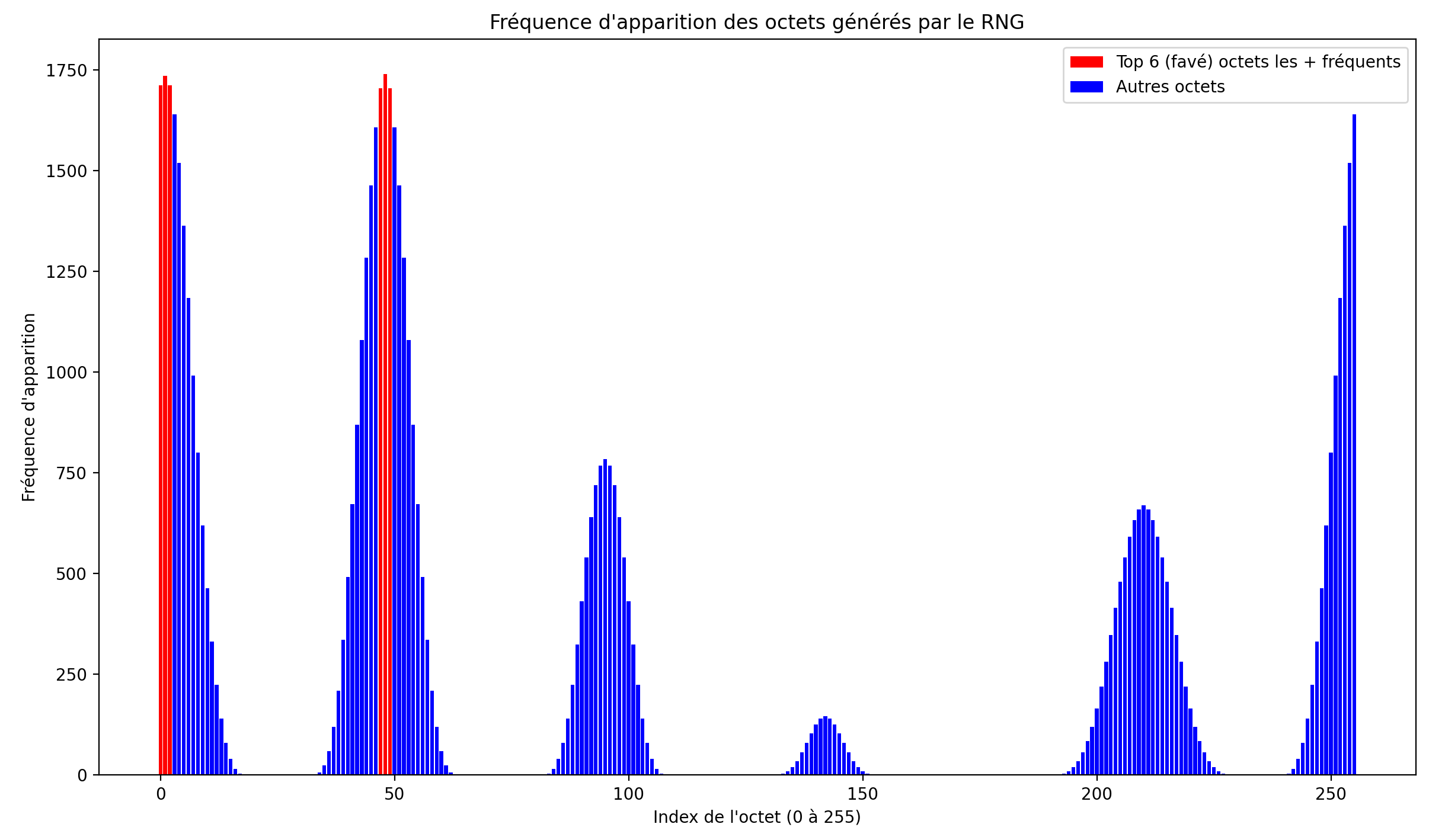
Le fichier chal.py implémente un RNG biaisé, en effet, un octet ($o$) est donné par la formule : $o = i + j + k + l \pmod{256}$. Avec $i, j, k, l$ des nombres tirés aléatoirement dans l’ensemble : $\lbrace48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 97, 98, 99, 100, 101, 102\rbrace$. Nous sommes donc loin d’une distribution uniforme.
Voici une image illustrant la proportion d’apparition des octets générés par ce RNG :
Une fois que nous connaissons les octets apparaissant les plus souvent, il suffit de demander un grand nombre de fois le flag chiffré pour voir quel octet ressort le plus. On saura donc que cet octet aura été chiffré avec un octet le plus fréquemment produit par le RNG.
Une analyse du biais du RNG est disponible dans le fichier analysis.py. L’implémentation de la solution qui exploite le biais est quant à elle disponible ci-dessous :
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
from pwn import process, remote
from hashlib import sha1
from tqdm import tqdm
from sys import argv
while True:
if len(argv) == 3:
conn = remote(argv[1], int(argv[2]))
elif len(argv) == 2:
conn = process(["python", argv[1]])
else:
print("Usage:")
print("python solve.py host port")
print("or")
print("python solve.py path-to-chal.py")
exit()
# skip header
conn.recvline()
def get_enc_flag() -> bytes:
conn.recvuntil(b"> ")
conn.sendline(b"again")
l = conn.recvline().strip()
l = bytes.fromhex(l.decode())
return l
def get_hint() -> bytes:
conn.recvuntil(b"> ")
conn.sendline(b"hint")
l = conn.recvline().strip()
l = bytes.fromhex(l.decode())
return l
sha1_flag = get_hint()
# on les connait grâce à analysis.py
possible_bytes = [47, 49, 0, 2, 1, 48]
all_enc_flag = []
flag_len = 70
print("Récupération de 50_000 chiffrés du flag...")
for _ in tqdm(range(50_000)):
all_enc_flag.append(get_enc_flag())
stats = [{k:0 for k in range(256)} for _ in range(flag_len)]
for aef in all_enc_flag:
for idx,val in enumerate(aef):
stats[idx][val] += 1
stats = [dict(sorted(s.items(), key=lambda item: item[1])) for s in stats]
build_flag = []
for st in stats:
stt = list(st.keys())[-1]
for pb in possible_bytes:
if pb ^ stt in [0, 255]:
build_flag.append(pb^stt)
bf = bytes(build_flag)
if len(bf) == flag_len and sha1_flag.hex() == sha1(bf).hexdigest():
print("interiut{" + bf.hex() + "}")
break
conn.close()